On cooking the primary reason for success is inspiration, in baking is measuring. By that of course I don’t mean that measuring is not required in cooking, but deviation from the original ratio of ingredients can be forgiving. And equally when baking inspiration is a key but deviating from the recipe ratio even for very little, will immediately cause inconsistencies in the outcome or even complete failure. So at the early age of baking and cooking the ratio and dosing of the ingredients became very significant and the cooks or the housewife will employ their homemade measuring device that will ensure that the quality will be consistent. Nowadays one more parameter became important temperature! In the modern kitchen, there are so many ways to measure something that you must have PhD in metrology. Join me to navigate to the wonderful world of metrology. No PhD required.
One gram is the absolute weight of a volume of pure water equal to the cube of the hundredth part of a metre, and at the temperature of melting ice.
There are two primary systems to measure ingredients weight and volume. Weight represents the mass of an item and currently there are two scales to measure it; the metric system followed by the majority of the world and the imperial system that is mainly found in the former colonies of the British empire. The fundamental difference between the two is the base unit of the systems and the fractions and multiples of the base units. So starting with the metric, the base is the gram (gm or g for short ) and is defined as “the absolute weight of a volume of pure water equal to the cube of the hundredth part of a metre, and at the temperature of melting ice” (later 4 °C). Currently a gram is defined as one one-thousandth of the SI base unit, the kilogram, or 1×10−3 kg, which itself is defined as being equal to the mass of a physical prototype preserved by the International Bureau of Weights and Measures. The divisions and multiples are products of ten and are used with the standard SI prefixes like n, μ, k, M, G etc. Off course in coking we will only need the kg which is the kilogram and is one thousand grams.
On the contrary the imperial system is more complicated and more elaborate. Even as early, as the end of the 19th and beginning of the 20th centuries, the UK was employing three different systems for mass and weight; a) troy weight, used for precious metals; b) avoirdupois weight, used for most other purposes; and c) apothecaries’ weight, now virtually unused since the metric system is used for all scientific purposes. The Weights and Measures Act 1855 (18 & 19 Victoria C72) made the avoirdupois pound the primary unit of mass. In all the systems, the fundamental unit is the pound, and all other units are defined as fractions or multiples of it. But, even the fractions and the multiples are not consistent so for example the next multiple is the stone that is 14 pounds, while the next fraction is the oz, where 16 oz make a pound.The pound has been officially defined in terms of the kilogram since the Mendenhall Order of 1893, to be 2.20462 pounds to a kilogram. It is not a very straight-forward measuring system, and that’s why many bakers prefer metric over it. Further the subdivision of the pound the oz is approximately 27 g which does not give to the baker the resolution required for the accuracy of the baking while the grain the next iteration is way to small (1/7000 lb). So with the metric system being in the appropriate resolution is no wonder that it has gained so much popularity among backers.
Comparing the two systems it is important to understand the mathematic delineation that characterizes the metric system based on the powers of 10 vs the imperial that quite empirical and it is based on the need to quantify things around certain range. As you can see in the following graph this is very well showcased. The is horizontal axis (x-axis) shows the three fractions and the three multiples of the unit, while the vertical axis (y-axis) shows the relation to the base unit (lb. vs g.). This by the way is called a log-scale; in a log scale equal distance means 10x. So two tick marks represent 100 times difference, while three is 1000 times.
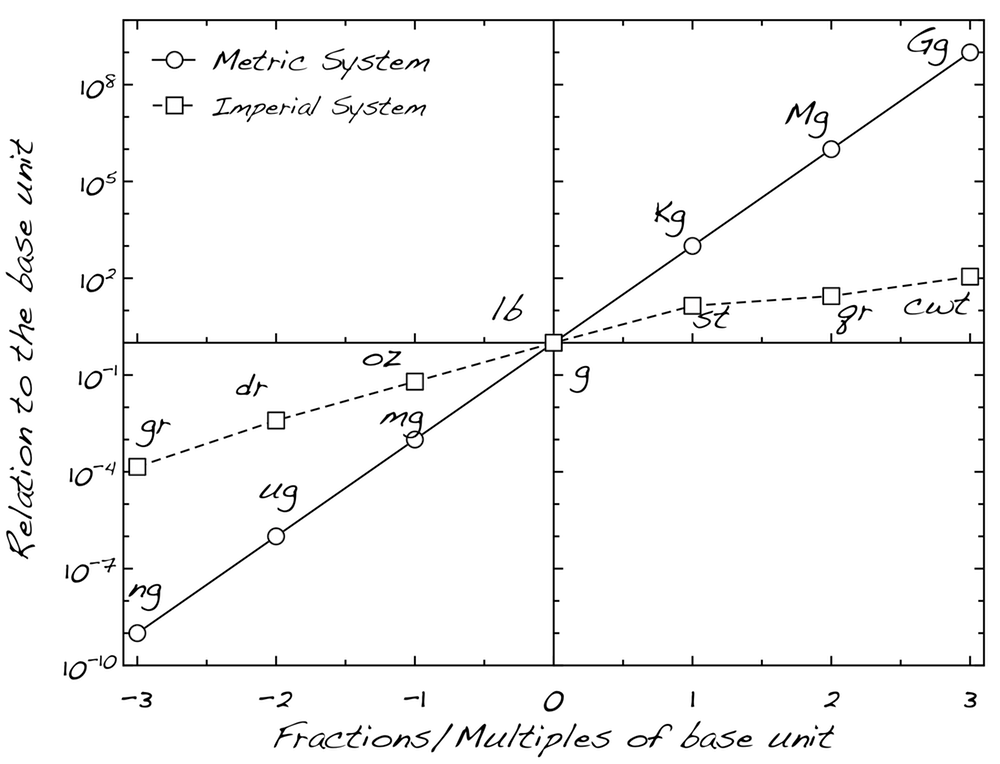
You can see that the Metric unit is on the same line, while the Imperial is not following a certain trend-line. At the end of the day, however, you can choose which ever you are more familiar with. I personally use both, metric for accuracy and imperial for the ease since sometimes the ration make so much more sense!
Weight Converter:
The pint’s a pound,
the world around
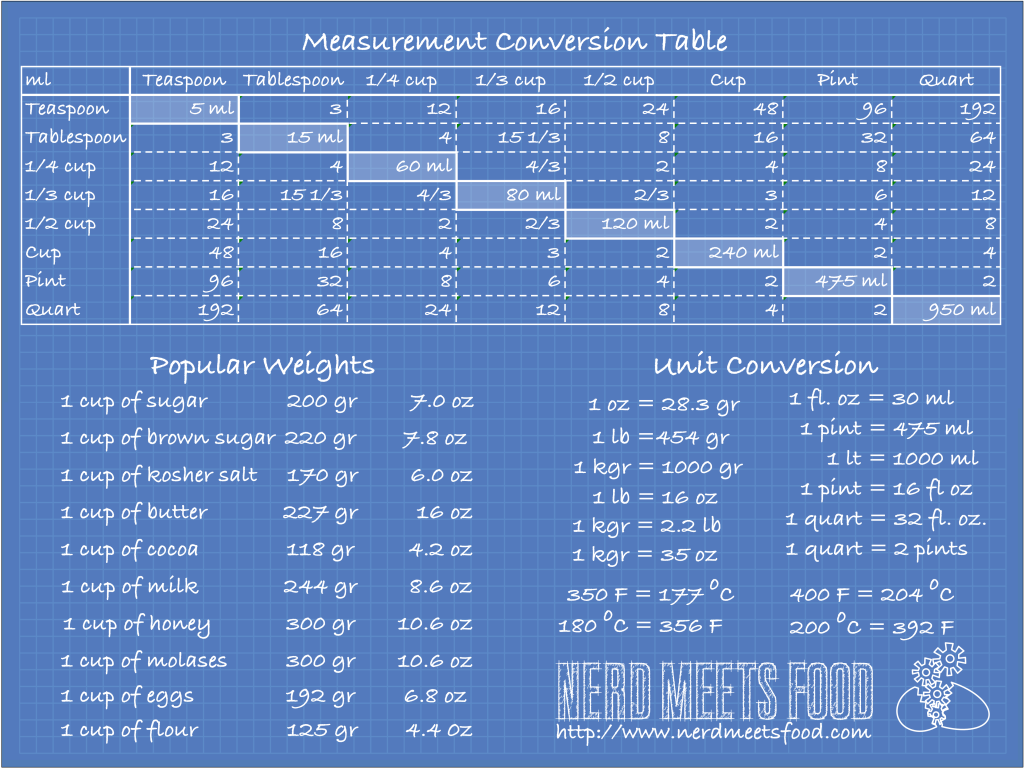
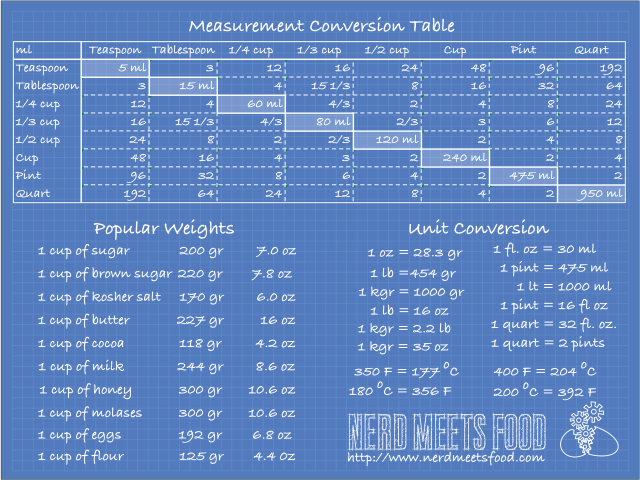
The other metric you should master is volume! Volume is still split between the imperial and metric system as before. However the volume is even more interesting. In the metric system the volume is directly the cube of the base length which is the meter (m3), but it is a little large (imagine that one cubic meter of water is 1 ton!). Instead the volume unit most commonly used is the litter and the ml (1/1000 of a litter) for smaller quantities. In the imperial system, the base length is the inch which by no means the cubic inch is the volume base unit. The assignments of volume quantities is completely random. The following table summarizes the relationship between these units.
| Unit | Imperial ounce |
Imperial pint |
Millilitres | Cubic inches | US ounces | US pints |
|---|---|---|---|---|---|---|
| fluid ounce (fl oz) | 1 | 1/20 | 28.4130625 | 1.7339 | 0.96076 | 0.060047 |
| gill (gi) | 5 | 1/4 | 142.0653125 | 8.6694 | 4.8038 | 0.30024 |
| pint (pt) | 20 | 1 | 568.26125 | 34.677 | 19.215 | 1.2009 |
| quart (qt) | 40 | 2 | 1,136.5225 | 69.355 | 38.430 | 2.4019 |
| gallon (gal) | 160 | 8 | 4,546.09 | 277.42 | 153.72 | 9.6076 |
| Note: The millilitre equivalences are exact, but cubic-inch and US measures are correct to 5 significant figures. | ||||||
Now that we know the basics of volumetric measurements we can provide an automatic converter that will convert between various quantities.
Volume Converter:
Recently, however, and by recently I mean probably the last 80 years or so, specially for baking and cooking in general there is a different unit commonly used, the cup. The measuring cup is a unit that was developed based on the imperial system (1 cup is 1/2 pint) but the fractions and of the cup were selected based on the quantities bakers and cooks more commonly use. So the teaspoon is approximately the amount of tea required for the perfect cup while the tablespoon is approximately the quantity that people are more comfortable having in their mouth when they are eating soup.
| cup | tablespoon | teaspoon | ml | oz | |
|---|---|---|---|---|---|
| cup | 1 | 16 | 48 | 236.6 | 8 |
| tablespoon | 16 | 1 | 3 | 14.79 | 1/2 |
| teaspoon | 48 | 3 | 1 | 4.93 | 1/6 |
And now that we have this out-of-the-way lets talk about something that is bugging me for a while now. Solid ingredients, like sugar, flour, nuts, rice etc measured with cups or other volume units. When the cup, a tool used in kitchen initially for liquids, made its way to the measurement of solids. So for example it made sense to use 1 cup of rice for two cups of water. However, measuring slides with volume results in inaccuracies. The primary reason for the inaccuracy is the packing factor. When you put particles of certain size in a container they interlock. However, their arrangement can result in different ways of packing them, and as a result the number of items you can fit. Imagine your clothes and a suitcase. When you just throw things in there vs. when you fold and neatly pack them. Same goes for sugar flour and all other granulated ingredients. The number of items you can fit in a volume is defined as the Random Close Packing (RCP). RCP is an empirical parameter that is the ratio of the volume of the items over the volume of the container. For perfect spheres of the same size it is 0.64 while for shapes like M&Ms is 0.68.
Most granules however don’t have a one size or a symmetric shape. The larger the size distribution the larger the RCP. This is more interesting when you thing that mechanical work changes packing. Have you noticed that when the coffee is not fitting in the jar you tap the jar and magically more coffee can fit. So packing can be very interesting parameter and one factor that can prevent consistent results. A common agreement is that you don’t pack the flour or the sugar, instead you aerate it. Further with a knife you can level of the container. Under these, and only these conditions we can somewhat accurately convert cup for mass. But even then you need to keep in mind that not all ingredients are exchanged equally. So a cup of flour is 128 g while a cup of sugar is 200 g. To even things out there is on term called density and is the ratio of the mass over the volume. Taking into consideration all these requirements and assumptions we can have a conversion table or even better a formula.
Universal ingredient converter:
This last formula took so long to develop that I am actually including it in the sidebar to help you convert recipes on the fly.
Finally this post would not be complete without referring to the other metric that defines cooking and baking, the temperature. It is imperative, especially for baking to set the right temperature in order to obtain the right texture and right consistency. This is true for everything from baking to grilling and even BBQ. Actually for most meats the temperature is something that is used to determine done-ness and safety. So it is very important to have a control over it and even more important to understand what it is about.
In our daily life we considered temperature to be an indication of how hot or cold is something. However, thermodynamics is defining temperature completely different. The law actually that defined temperature was put in place after the first, second and third law of thermodynamics, but it is essential to understand the other three laws, so it was brilliantly named zeroth, in order to proceed them. The zeroth law of thermodynamics states that when systems, A and B, are in thermal equilibrium with each other, and B is in thermal equilibrium with a third system, C, then A is also in thermal equilibrium with C. Two systems are in thermal equilibrium if they could transfer heat between each other, but don’t. I know there is not temperature defined in there, but it was introduced right after as a measure of the thermal equilibrium. Heat will always transfer from the higher temperature to the lower temperature. So how does this translates to real life? By itself temperature of 21 C (70 F) means nothing. Yes, for most of the people is a quite comfortable temperature. But what is a comfortable temperature? It is the temperature that allows heat transfer from the body to the environment without any significant effort. Lower temperature and the body cannot produce enough heat to replenish the one lost and higher will make us hot. So basically temperature dictates the thermal exchange with the environment. All the changes that happen to food at specific temperature happens because enough energy was supplied to the molecules to initiate them. So for example 160 F is the temperature that the proteins have absorbed enough heat to change the chemical structure. At similar temperature the energy that has been supplied is sufficient to break the molecular structure of bacteria and make the food safe.
Andres Celcius created a scale to define temperature. He set the 0 at the temperature that enough heat has been lost from water to adequately drop its energy to convert it to solid. Similarly he set the 100 of the scale as the temperature that water adsorbed enough heat to convert it to vapor (boiling point). And thus the Celsius scale was born. On a different day a different guy Mr. Fahrenheit defined zero on its scale as the temperature he assumed it can be the lowest he ever experienced. Similarly he defined the 100 as the hottest fever he ever had. And thus the Fahrenheit was born. And the conversion from one to the other is not as simple, as let’s say the lbs to kg. This is a linear conversion but it also has an offset.

The diagram here shows side by side the two different scales highlighting the major points like the freezing and the boiling of the water. It also highlights the most common setting for ovens and the temperature that a broiler is using. It is valuable to have a small conversion for the temperature as well.
Temperature conversion tool:
So here you have it! All you need to know about the basics of culinary metrology. And as a bonus you can get the great picture that shown in the top of the article right here. Print it, Frame it and post it in your kitchen.